八年级数学《勾股定理》教案6篇(《勾股定理》八年级数学教案：6篇精选，助你轻松掌握)

Youaremine 2024-02-15

本文为公文网站地编辑，将为大家介绍八年级数学《勾股定理》教案6篇。这些教案旨在帮助八年级学生深入理解勾股定理的概念和应用，提供了丰富的教学资源和实例，帮助学生掌握解题技巧。无论是教师还是学生，都能从这些教案中获得宝贵的学习经验和启发。

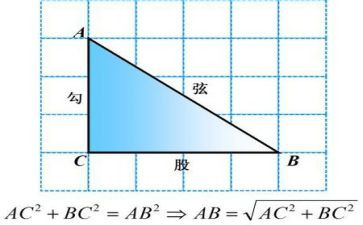
八年级数学《勾股定理》教案篇1

教学目标

知识与技能：

了解勾股定理的一些证明方法，会简单应用勾股定理解决问题

过程与方法：

在充分观察、归纳、猜想的基础上，探究勾股定理，在探究的过程中，发展合情推理，体会数形结合、从特殊到一般等数学思想。

情感态度价值观：

通过对我国古代研究勾股定理的成就介绍，培养学生的民族自豪感。

教学过程

1、创设情境

问题1国际数学家大会是最高水平的全球性数学学科学术会议，被誉为数学界的“奥运会”。2002年在北京召开了第24届国际数学家大会。下图就是大会会徽的`图案。你见过这个图案吗？它由哪些我们学习过的基本图形组成？这个图案有什么特别的含义？

师生活动：教师引导学生寻找图形中的直角三角形和正方形等，并引导学生发现直角三角形的全等关系，指出通过今天的学习，就能理解会徽图案的含义。

设计意图：本节课是本章的起始课，重视引言教学，从国际数学家大会的会徽说起，设置悬念，引入课题。

2、探究勾股定理

观看洋葱数学中关于勾股定理引入的视频，让我们一起走进神奇的数学世界

问题2相传2500多年前，毕达哥拉斯有一次在朋友家作客时，发现朋友家用转铺成的地面图案反应了直角三角形三边的某种数量关系，请你观察下图，你从中发现了什么数量关系？

师生活动：学生先独立观察思考一分钟后，小组交流合作分析图形中两个蓝色正方形与橙色正方形有哪些数量关系，教师参与学生的讨论

追问：由这三个正方形的边长构成的等腰直角三角形三条边长之间又有怎么样的关系？

师生活动：教师引导学生发现正方形的面积等于边长的平方，归纳出：等腰直角三角形两条直角边的平方和等于斜边的平方。

设计意图：从最特殊的等腰直角三角形入手，便于学生观察得到结论

问题3：数学研究遵循从特殊到一般的数学思想，既然我们得到了等腰直角三角形三边的这种特殊的数量关系，那我们不妨大胆猜测在一般的直角三角形（在下图的方格纸中，每个方格的面积是1）中，这种特殊的数量关系也同样成立。

师生活动：学生独立思考后小组讨论，难点是如何证明求以斜边为边长的正方形的面积，可由师生共同总结得出可以通过割、补两种方法，求出其面积。

八年级数学《勾股定理》教案篇2

教学目标

1、知识与技能目标

学会观察图形，勇于探索图形间的关系，培养学生的空间观念、

2、过程与方法

（1）经历一般规律的探索过程，发展学生的抽象思维能力、

（2）在将实际问题抽象成几何图形过程中，提高分析问题、解决问题的能力及渗透数学建模的思想、

3、情感态度与价值观

（1）通过有趣的问题提高学习数学的兴趣、

（2）在解决实际问题的过程中，体验数学学习的实用性、

教学重点：

探索、发现事物中隐含的勾股定理及其逆及理，并用它们解决生活实际问题、

教学难点：

利用数学中的建模思想构造直角三角形，利用勾股定理及逆定理，解决实际问题、

教学准备：

多媒体课件

教学过程：

第一环节：创设情境，引入新课（3分钟，学生观察、猜想）

情景：

如图：在一个圆柱石凳上，若小明在吃东西时留下了一点

食物在B处，恰好一只在A处的蚂蚁捕捉到这一信息，于

是它想从A处爬向B处，你们想一想，蚂蚁怎么走最近？

第二环节：合作探究（15分钟，学生分组合作探究）

学生分为４人活动小组，合作探究蚂蚁爬行的最短路线，充分讨论后，汇总各小组的方案，在全班范围内讨论每种方案的路线计算方法，通过具体计算，总结出最短路线。让学生发现：沿圆柱体母线剪开后展开得到矩形，研究“蚂蚁怎么走最近”就是研究两点连线最短问题，引导学生体会利用数学解决实际问题的方法：建立数学模型，构图，计算、

学生汇总了四种方案：

（１）（２）（

学生很容易算出：情形（１）中A→B的路线长为：AA’+d，

情形（２）中A→B的路线长为：AA’+πd／2

所以情形（１）的路线比情形（２）要短、

学生在情形（３）和（４）的比较中出现困难，但还是有学生提出用剪刀沿母线AA’剪开圆柱得到矩形，前三种情形A→B是折线，而情形（４）是线段，故根据两点之间线段最短可判断（４）最短、

如图：

（１）中A→B的路线长为：AA’+d；

（２）中A→B的路线长为：AA’+A’B>AB；

（３）中A→B的路线长为：AO+OB>AB；

（４）中A→B的路线长为：AB。

得出结论：利用展开图中两点之间，线段最短解决问题、

在这个环节中，可让学生沿母线剪开圆柱体，具体观察、

接下来后提问：怎样计算AB？

在Rt△AA′B中，利用勾股定理可得，若已知圆柱体高为12cm，底面半径为3cm，π取3，则。

第三环节：做一做（7分钟，学生合作探究）

教材23页

李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB，但他随身只带了卷尺，

（1）你能替他想办法完成任务吗？

（2）李叔叔量得AD长是30厘米，AB长是40厘米，BD长是50厘米，AD边垂直于AB边吗？为什么？

（3）小明随身只有一个长度为20厘米的刻度尺，他能有办法检验AD边是否垂直于AB边吗？BC边与AB边呢？

第四环节：巩固练习（10分钟，学生独立完成）

1、甲、乙两位探险者到沙漠进行探险，某日早晨8：00甲先出发，他以6km/h的速度向正东行走，1小时后乙出发，他以5km/h的速度向正北行走、上午10：00，甲、乙两人相距多远？

2、如图，台阶A处的蚂蚁要爬到B处搬运食物，它怎么走最近？并求出最近距离、

3、有一个高为1。5米，半径是1米的圆柱形油桶，在靠近边的地方有一小孔，从孔中插入一铁棒，已知铁棒在油桶外的部分为0。5米，问这根铁棒有多长？

第五环节课堂小结（3分钟，师生问答）

内容：

1、如何利用勾股定理及逆定理解决最短路程问题？

第六环节：布置作业（2分钟，学生分别记录）

内容：

作业：1、课本习题1、5第1，2，3题、

要求：A组（学优生）：1、2、3

B组（中等生）：1、2

C组（后三分之一生）：1

八年级数学《勾股定理》教案篇3

一、教学目标

1、让学生通过对的图形创造、观察、思考、猜想、验证等过程，体会勾股定理的产生过程。

2、通过介绍我国古代研究勾股定理的成就感培养民族自豪感，激发学生为祖国的复兴努力学习。

3、培养学生数学发现、数学分析和数学推理证明的能力。

二、教学重难点

利用拼图证明勾股定理

三、学具准备

四个全等的直角三角形、方格纸、固体胶

四、教学过程

(一) 趣味涂鸦，引入情景

教师：很多同学都喜欢在纸上涂涂画画，今天想请大家帮老师完成一幅涂鸦，你能按要求完成吗?

(1)在边长为1的方格纸上任意画一个顶点都在格点上的直角三角形。

(2)再分别以这个三角形的三边向三角形外作3个正方形。

学生活动：先独立完成，再在小组内互相交流画法，最后班级展示。

(二)小组探究，大胆猜想

教师：观察自己所涂鸦的图形，回答下列问题：

1、请求出三个正方形的面积，再说说这些面积之间具有怎样的数量关系?

2、图中所画的直角三角形的边长分别是多少?请根据面积之间的关系写出边长之间存在的数量关系。

3、与小组成员交流探究结果?并猜想：如果直角三角形两直角边分别为a、b,斜边为c，那么a，b，c具有怎样的数量关系?

4、方法提炼：这种利用面积相等得出直角三角形三边等量关系的方法叫做什么方法?

学生活动：先独立思考，再在小组内互相交流探究结果，并猜想直角三角形的三边关系，最后班级展示。

(三)趣味拼图，验证猜想

教师：请利用四个全等的直角三角形进行拼图。

1、你能拼出哪些图形?能拼出正方形和直角梯形吗?

2、能否就你拼出的图形利用面积法说明a2+b2=c2的合理性?如果可以，请写下自己的推理过程。

学生活动：独立拼图，并思考如何利用图形写出相应的证明过程，再在组内交流算法，最后在班级展示。

(四)课堂训练巩固提升

教师：请完成下列问题，并上台进行展示。

1.在Rt△ABC中,∠C=900,∠A,∠B,∠C的对边分别为a,b,c

已知a=6,b=8.求c.

已知c=25,b=15.求a .

已知c=9,a=3.求b.(结果保留根号)

学生活动：先独立完成问题，再组内交流解题心得，最后上台展示，其他小组帮助解决问题。

(五)课堂小结，梳理知识

教师：说说自己这节课有哪些收获?请从数学知识、数学方法、数学运用等方向进行总结。

八年级数学《勾股定理》教案篇4

教学目标

1、知识与技能目标：探索并理解直角三角形的三边之间的数量关系，通过探究能够发现直角三角形中两个直角边的平方和等于斜边的平方和。

2、过程与方法目标：经历用测量和数格子的办法探索勾股定理的过程，进一步发展学生的合情推理能力。

3、情感态度与价值观目标：通过本节课的学习，培养主动探究的习惯，并进一步体会数学与现实生活的紧密联系。

教学重点

了解勾股定理的由来，并能用它来解决一些简单的问题。

教学难点

勾股定理的探究以及推导过程。

教学过程

一、创设问题情景、导入新课

首先出示：投影1（章前的图文）并介绍我国古代在勾股定理研究方面的贡献，结合课本第六页谈一谈我国是最早了解勾股定理的国家之一，介绍商高（三千多年前周期的数学家）在勾股定理方面的贡献。

出示课件观察后回答：

1、观察图1—2，正方形A中有_______个小方格，即A的面积为______个单位。

正方形B中有_______个小方格，即B的面积为______个单位。

正方形C中有_______个小方格，即C的面积为______个单位。

2、你是怎样得出上面的结果的？

3、在学生交流回答的基础上教师进一步设问：图1—2中，A，B，C面积之间有什么关系？学生交流后得到结论：A+B=C。

二、层层深入、探究新知

1、做一做

出示投影3（书中P3图1—3）

提问：（1）图1—3中，A，B，C之间有什么关系？（2）从图1—2，1—3中你发现什么？

学生讨论、交流后，得出结论：以三角形两直角边为边的正方形的面积和，等于以斜边为边的正方形面积。

2、议一议

图1—2、1—3中，你能用三角形的边长表示正方形的面积吗？

（1）你能发现直角三角形三边长度之间的关系吗？在同学交流的基础上，共同探讨得出：直角三角形两直角边的平方和等于斜边的平方。这就是著名的“勾股定理”。也就是说如果直角三角形的两直角边为a，b，斜边为c那么。我国古代称直角三角形的较短的直角边为勾，较长的为股，斜边为弦，这就是勾股定理的由来。

（2）分别以5厘米和12厘米为直角边做出一个直角三角形，并测量斜边的长度（学生测量后回答斜边长为13）请大家想一想（2）中的规律，对这个三角形仍然成立吗？

3、想一想

我们常见的电视的尺寸：29英寸（74厘米）的电视机，指的是屏幕的长吗？还是指的.是屏幕的宽？那他指什么呢？能否运用刚才所学的知识，检验一下电视剧的尺寸是否合格？

三、巩固练习。

1、在图1—1的问题中，折断之前旗杆有多高？

2、错例辨析：△ABC的两边为3和4，求第三边

解：由于三角形的两边为3、4

所以它的第三边的c应满足

=25即：c=5辨析：（1）要用勾股定理解题，首先应具备直角三角形这个必不可少的条件，可本题三角形ABC并未说明它是否是直角三角形，所以用勾股定理就没有依据。（2）若告诉△ABC是直角三角形，第三边C也不一定是满足，题目中并未交待C是斜边。

综上所述这个题目条件不足，第三边无法求得

四、课堂小结

鼓励学生自己总结、谈谈自己本节课的收获，以及自己对勾股定理的理解，老师加以纠正和补充。

五、布置作业

八年级数学《勾股定理》教案篇5

课题：

勾股定理

课型：

新授课

课时安排：

1课时

教学目的：

一、知识与技能目标理解和掌握勾股定理的内容，能够灵活运用勾股定理进行计算，并解决一些简单的实际问题。

二、过程与方法目标通过观察分析，大胆猜想，并探索勾股定理，培养学生动手操作、合作交流、逻辑推理的能力。

三、情感、态度与价值观目标了解中国古代的数学成就，激发学生爱国热情；学生通过自己的努力探索出结论获得成就感，培养探索热情和钻研精神；同时体验数学的美感，从而了解数学，喜欢几何。

教学重点：

引导学生经历探索及验证勾股定理的过程，并能运用勾股定理解决一些简单的实际问题

教学难点：

用面积法方法证明勾股定理

课前准备：

多媒体ppt，相关图片

教学过程：

（一）情境导入

1、多媒体课件放映图片欣赏：勾股定理数形图，1955年希腊发行的一枚纪念邮票，美丽的勾股树，2002年国际数学大会会标等。通过图形欣赏，感受数学之美，感受勾股定理的文化价值。

2、多媒体课件演示FLASH小动画片：某楼房三楼失火，消防队员赶来救火，了解到每层楼高3米，消防队员取来6.5米长的云梯，如果梯子的底部离墙基的距离是2.5米，请问消防队员能否进入三楼灭火？已知一直角三角形的.两边，如何求第三边？学习了今天的这节课后，同学们就会有办法解决了。

（二）学习新课问题一是等腰直角三角形的情形（通过多媒体给出图形），判断外围三个正方形面积有何关系？相传2500年前，毕达哥拉斯（古希腊著名的哲学家、数学家、天文学家）有一次在朋友家做客时，发现朋友家里用砖铺成的地面中反映了直角三角形三边的某种数量关系。你能观察图中的地面，看看能发现什么？对于等腰直角三角形有这样的性质：两直边的平方和等于斜边的平方那么对于一般的直角三角形是否也有这样的性质呢？请大家画一个任意的直角三角形，量一量，算一算。问题二是一般直角三角形的情形，判断这时外围三个正方形的面积是否也存在这种关系？通过这个观察和验算这个直角三角形外围的三个正方形面积之间的关系，同学们发现了什么规律吗？通过前面对两个问题的验证，可以得到勾股定理：如果直角三角形的两直角边长分别为a、b，斜边为c，那么a2+b2=c2。

（三）巩固练习1、如果一个直角三角形的两条边长分别是6厘米和8厘米，那么这个三角形的周长是多少厘米？2、解决课程开始时提出的情境问题。

（四）小结

1、背景知识介绍①《周髀算径》中，西周的商高在公元一千多年前发现了“勾三股四弦五”这一规律；②康熙数学专著《勾股图解》有五种求解直角三角形的方法，积求勾股法是他的独创。

2、通过这节课的学习，你会写方程了吗？你有什么收获和体会？

（五）作业练习18.1中的1、2、3题。板书设计：勾股定理：如果直角三角形的两直角边长分别为a、b，斜边为c，那么a2+b2=c2。

八年级数学《勾股定理》教案篇6

教学目标：

理解并掌握勾股定理及其证明。在学生经历“观察—猜想—归纳—验证”勾股定理的过程中，发展合情推理能力，体会数形结合和从特殊到一般的思想。通过对勾股定理历史的了解，感受数学文化，激发学习兴趣；在探究活动中，培养学生的合作交流意识和探索精神

重点

探索和证明勾股定理。

难点

用拼图方法证明勾股定理。